logo image

[baekjoon] - C++ 백준 6198번: 옥상 정원

image of C++ 백준 6198번: 옥상 정원

바킹독 문제집 - 스택 을 푸는데, 백준 6198 문제에서 막혔다.
아니 어떻게 스택을 이용해서 풀어야 하는거지? 하고 참고를 했는데, 이 문제는 생각의 전환이 필요했다.

§아이디어

예를 들어, N=6, H = { 10, 3, 7, 4, 12, 2 }인 경우를 보자. 높이가 10인 건물은 높이가 3, 7, 4인 건물 3개를 볼 수 있다. 마찬가지로, 높이가 3인 건물은 0개의 건물을 보고, 7인 건물은 1개의 건물을 볼 수 있다.

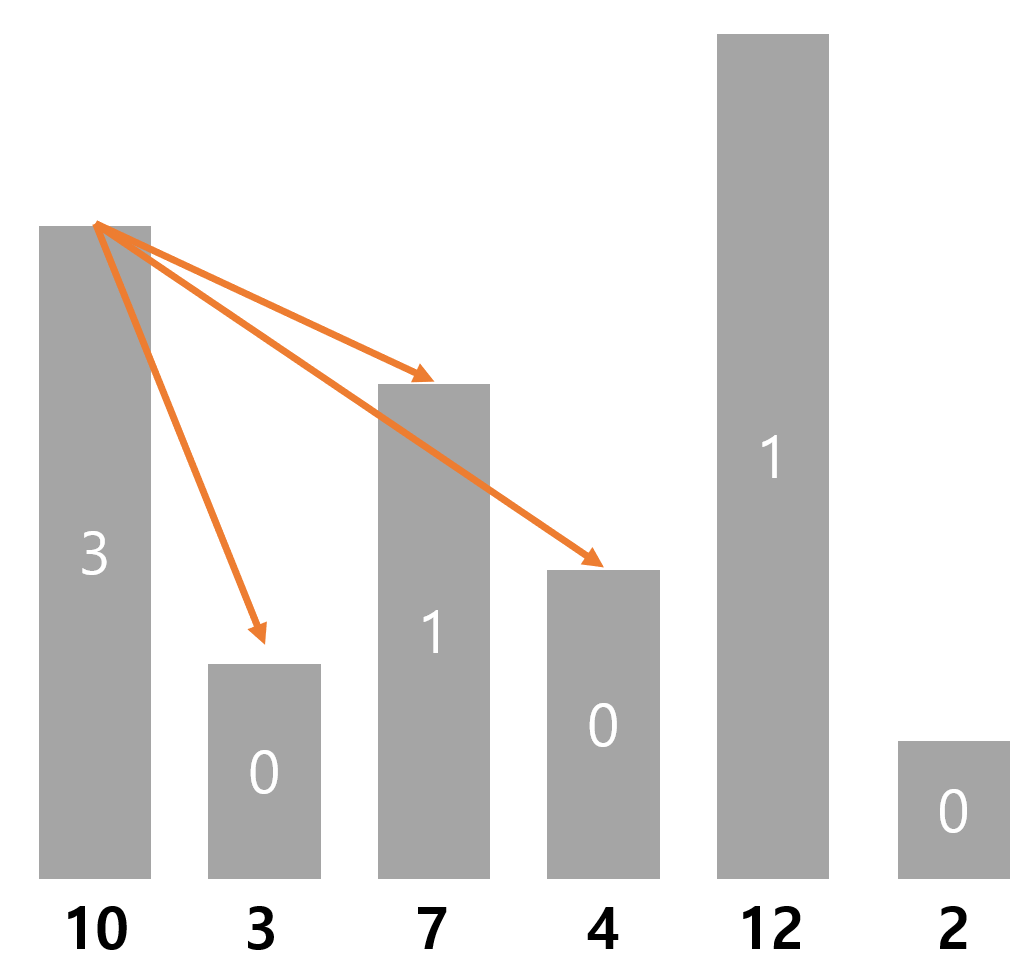각 건물이 보는 건물 수 하지만, 이렇게 생각하면 최소 2중 반복문을 사용하여, 매 높이를 비교하며 개수를 각각 구해야 한다. (이렇게 했다가 시간 초과 남)

스택을 사용하기 위해서는 생각의 전환이 필요하다! 이제부터는 각 건물이 볼 수 있는 건물 개수가 아닌, 몇 개의 건물로부터 보여짐을 당하고 있는가? 라고 생각한다.

예를 들어, 높이가 10인 건물은 3개를 보지만, 0개의 건물로부터 보여짐을 당한다. 높이가 3과 7인 건물은 1 (10)개의 건물로부터 보여짐을 당하고, 높이가 4인 건물은 2 (10, 7)개의 건물로부터 보여짐을 당한다.

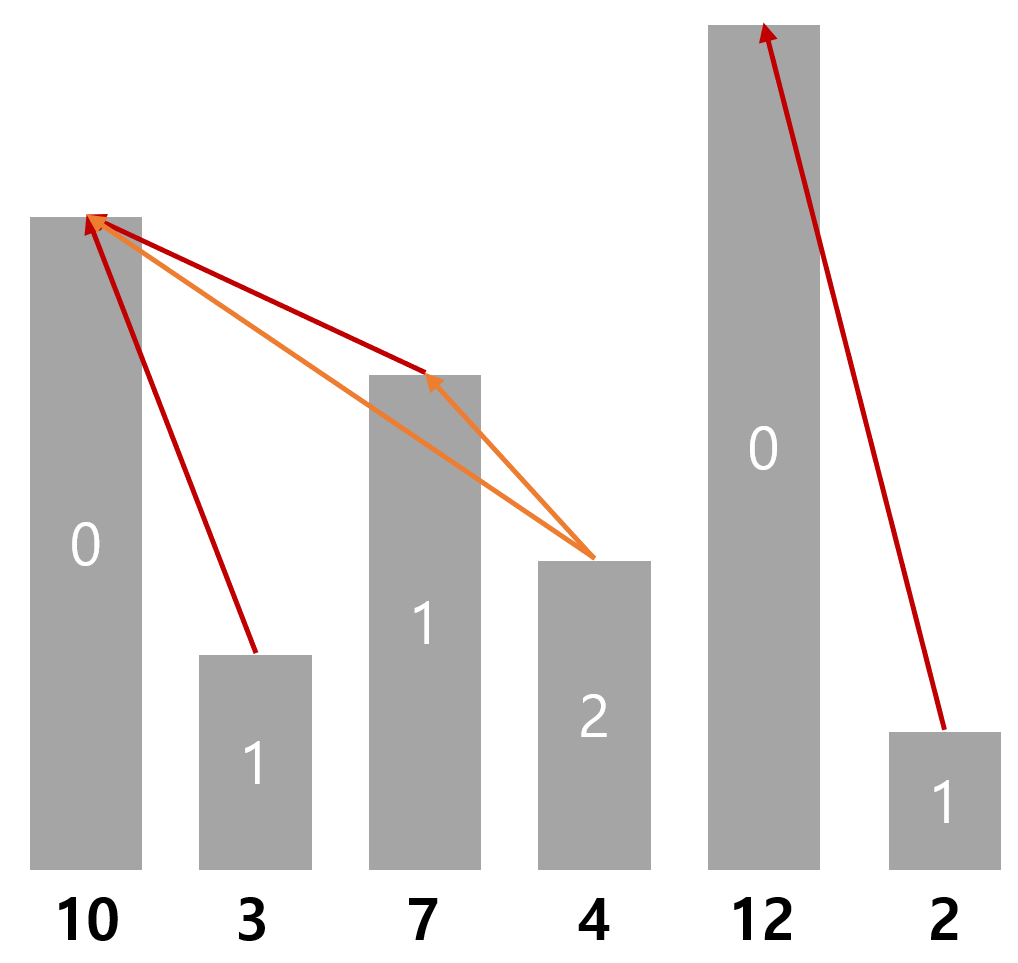각 건물이 보여지는 건물 수 결국 각 높이를 입력할 때마다, 스택에 넣고, 만약 현재 높이가 스택의 탑 부분보다 같거나 크다면 pop() 으로 빼준다. 그렇게 했을 때, 스택에 남아있는 숫자(높이) 개수가 현재 나를 보고 있는 건물 수이다.

현재 높이가 가장 크다면, stack은 당연히 비어있게 되고, 자신을 보는 건물개수도 0개가 된다.

§왜 스택을 쓰는가? - !! 매우 개인적인 생각 !!

뭔가 논리적인 비약이 크다. 근데 곱씹어 생각해 봤을 때, { 10, 3, 7, 4 } 구간에서 높이가 7인 건물은 3보다 같거나 크므로, 3은 스택에서 제거가 되며 7은 스택에 넣어진다. 그리고 스택에는 { 10, 7 } 만 남아있다.

일반적으로 생각했을 때, 다음 높이가 4인 건물의 입장에서 보았을 때도, 높이가 3인 건물은 높이가 7인 건물에 의해 가려지므로, 3 건물은 4 건물에 당연히 보여지지 않는 건물이다.

그래서 요약하자면, 다음과 같은 상황에서 스택이 적절히 사용될 수 있다고 생각했다.

  1. 현재 내 값으로 인해 이전 값이 필요 없어질 때 (ex. 높이 7에 의해 높이 3 건물은 필요 없어짐)
  2. 조건이 한 방향 으로만 진행된다고 보장될 때 (스택의 특성 LIFO)

§C++ 코드

참고로 answer 변수는 long long 타입을 사용했다.

조건이

    1. 첫 번째 줄에 빌딩의 개수 N이 입력된다.(1 ≤ N ≤ 80,000)
    1. 두 번째 줄 부터 N+1번째 줄까지 각 빌딩의 높이가 hi 입력된다. (1 ≤ hi ≤ 1,000,000,000)

인데, 높이가 { 1000000000-1, 1000000000-2, 1000000000-3, ..., 1000000000 - 80000 } 순으로 되어있다면, 각각 answer 값은 79999 + 79998 + ... + 0 == (약 64억)/2 이 될 것이다. int 나 unsigned int의 최대값은 각각 약 21억과 42억정도 이므로 저 64억짜리 값을 담아내긴 어렵다. 따라서 그보다 더 큰 long long 으로 선언해야 한다!

#include <bits/stdc++.h>
using namespace std;
 
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
 
    int N, height;
    cin >> N;
 
    // 꼭 long long
    long long answer = 0;
    stack<int> s;
    while(N--) {
        cin >> height;
        while(!s.empty() && s.top() <= height) s.pop();
 
        answer += s.size();
        s.push(height);
    }
 
    cout << answer;
}

Loading Comments...